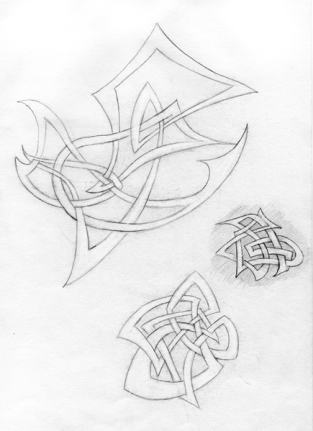If you’ve ever enjoyed a wide-eyed look at ‘The Book Of Kells’, or any of the intricate knot-work of Celtic origin, you’ll understand my fascination with drawing knots… The Tibetans also have an ‘auspicious symbol’ known as an infinite knot, which symbolizes continuity, cause and effect, and the interconectedness of all things.
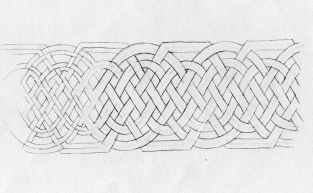
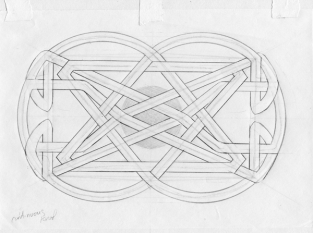
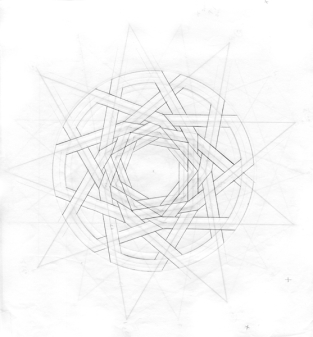
Various knot systems have their ‘rules’, or types of order which impart to them their own sense of beauty and harmony.
My favorite of these ‘rules’ is as follows:
- Every time a strand crosses another strand, it must alternate between crossing over or under the other strand. Think of it as if you are travelling down a long winding road — each time you come to an intersection, you will be crossing over or under a bridge. You can’t cross over two bridges in a row, nor can you cross under two bridges in a row. Not in the world of continuous knots!
- The knot must have no beginning and no end — like a circle it is continuous. The road you are travelling will eventually return to its own beginning.
This creates a challenging but satisfying puzzle to ‘solve’, while at the same time working with one’s own aesthetic sensibility.
Below are some examples of my knot experiments. Some were built upon definite geometric underpinnings, while some were completely free-form. The free-form examples were, I must admit, made to pass the time at a few long lectures I attended. Not that the lectures weren’t interesting, but somehow the absorption of the knots helped me pay attention…